现实世界几乎所有实际系统本质上均具有空间分布特征，其系统状态不仅与时间有关还依赖于空间位置，比如化工过程、振动过程(包括弦振动、梁振动、波动)、核反应过程等。这类系统称为分布参数系统(Distributed Parameter Systems, DPS)。不同于由常微分方程(Ordinary Differential Equation, ODE) 描述的集中参数系统(Lumped ParameterSystems, LPS)，DPS 通常是由偏微分方程(Partial Differential Equation, PDE)或偏微分-常微分方程或积分-微分方程或抽象空间中的微分方程描述。DPS 有时也称为无穷维系统，这是因为相较于具有有限个自由度的LPS，此类系统具有无穷多个自由度。囿于数学工具，有时候人们会把DPS 控制问题简化成LPS 来处理。这是因为对于LPS 的控制，已经有了相对完善的解决方案。一般来说，对于一个DPS，为了得到更好的控制效果与更高的精确度，有必要直接从DPS 的原始模型出发来解决其控制问题。这样做也可以从根本上避免因采用有限维简化模型而出现控制溢出与观测溢出等现象。

        LPS的状态空间为标准欧式空间。在此空间上，不同范数是等价的。而此良好性质在无穷维泛函空间上不成立，这增加了定义在无穷维泛函空间上的DPS分析与控制设计困难。即使是最简单DPS稳定性分析，也难以建立像LPS中统一的稳定性分析结果。这是因为在泛函空间上，用不同范数定义稳定性是不等价的，DPS稳定性分析在不同范数意义下分别讨论。另外，用于刻画DPS无穷维动态的PDE模型也是千差万别。PDE即使形式相近，性质也会完全不同，如z_t(x, t) = z_xx(x, t)（热方程）、z_t(x, t) = -z_x(x, t)（一阶双曲型方程）和z_tt(x, t) = z_xx(x, t)（波方程）。这三类方程形式相近，但性质却完全不同，如热方程的特征值均为实数、一阶双曲型方程的特征实部为负无穷大而波方程的特征值实部均为零。因此，DPS稳定性分析与控制需要根据PDE模型具体问题具体分析。

        针对不同PDE模型，在不同范数意义下，开展DPS分析与控制研究工作，主要包括

        在该方向，已取得阶段性研究进展：

• 利用基于观测器的输出反馈控制技术解决由控制驱动与测量输出非同位导致的控制设计困难（Jun-Wei Wang*, A unified Lyapunov-based design for a dynamic compensator of linear parabolic MIMO PDEs, International Journal of Control, vol. 94, no. 7, pp. 1804-1811, 2021.）；

• 
  

• 针对著名的庞加莱-温格尔不等式，给出其变种形式（一维空间，高维空间），以克服由有限维控制输入和测量输出导致的闭环控制系统分析困难（Jun-Wei Wang*, Dynamic boundary fuzzy control design of semi-linear parabolic PDE systems with spatially non-collocated discrete observation, IEEE Transactions on Cybernetics, vol. 49, no. 8, pp. 3041-3051, 2019. Jun-Wei Wang* and Jun-Min Wang, Dynamic compensator design of linear parabolic MIMO PDEs in N-dimensional spatial domain, IEEE Transactions on Automatic Control, vol. 66, no. 3, pp. 1399-1406, 2021.）；

• 一维空间
  

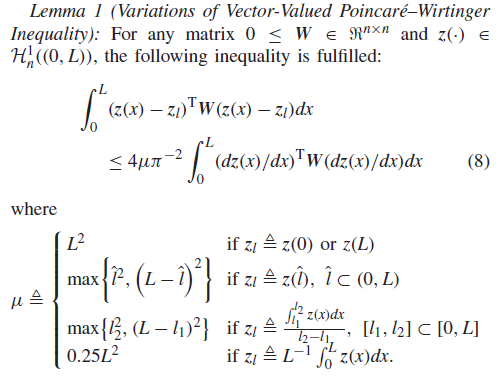
• 高维空间

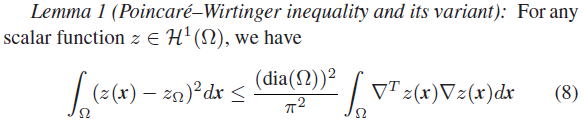
• 引入多智能体一致性理论，针对多输入多输出线性PDE协同控制策略，以提升相应闭环PDE系统空间一致性能（Jun-Wei Wang, Yang Yang, and Qing-Long Zhang, Cooperative control and centralized state estimation of a linear parabolic PDE under a directed communication topology, IFAC-PapersOnLine, vol. 55, no. 26, pp. 131-136, 2022. Jun-Wei Wang, Coordination of actuator-plus-sensor networks for control and estimation performance improvement in linear distributed parameter systems, https://www.researchgate.net/publication/362248268.）。